Advanced Features

We now turn to some of Tamarin’s more advanced features. We cover custom heuristics, the GUI, channel models, induction, internal preprocessor, and how to measure the time needed for proofs.

Heuristics

A heuristic describes a method to rank the open goals of a constraint system and is specified as a sequence of goal rankings. Each goal ranking is abbreviated by a single character from the set {s,S,c,C,i,I,o,O}.

A global heuristic for a protocol file can be defined using the heuristic: statement followed by the sequence of goal rankings. The heuristic which is used for a particular lemma can be overwritten using the heuristic lemma attribute. Finally, the heuristic can be specified using the --heuristic command line option.

The precedence of heuristics is:

1. Command line option (--heuristic)
2. Lemma attribute (heuristic=)
3. Global (heuristic:)
4. Default (s)

The goal rankings are as follows.

s:

the ‘smart’ ranking is the ranking described in the extended version of our CSF’12 paper. It is the default ranking and works very well in a wide range of situations. Roughly, this ranking prioritizes chain goals, disjunctions, facts, actions, and adversary knowledge of private and fresh terms in that order (e.g., every action will be solved before any knowledge goal). Goals marked ‘Probably Constructable’ and ‘Currently Deducible’ in the GUI are lower priority.

S:

is like the ‘smart’ ranking, but does not delay the solving of premises marked as loop-breakers. What premises are loop breakers is determined from the protocol using a simple under-approximation to the vertex feedback set of the conclusion-may-unify-to-premise graph. We require these loop-breakers for example to guarantee the termination of the case distinction precomputation. You can inspect which premises are marked as loop breakers in the ‘Multiset rewriting rules’ page in the GUI.

c:

is the ‘consecutive’ or ‘conservative’ ranking. It solves goals in the order they occur in the constraint system. This guarantees that no goal is delayed indefinitely, but often leads to large proofs because some of the early goals are not worth solving.

C:

is like ‘c’ but without delaying loop breakers.

i:

is a ranking developed to be well-suited to injective stateful protocols. The priority of goals is similar to the ‘S’ ranking, but instead of a strict priority hierarchy, the fact, action, and knowledge goals are considered equal priority and solved by their age. This is useful for stateful protocols with an unbounded number of runs, in which for example solving a fact goal may create a new fact goal for the previous protocol run. This ranking will prioritize existing fact, action, and knowledge goals before following up on the fact goal of that previous run. In contrast the ‘S’ ranking would prioritize this new fact goal ahead of any existing action or knowledge goal, although solving the new goal may create yet another earlier fact goal and so on, preventing termination.

I:

is like ‘i’ but without delaying loop breakers.

{.}:

is the tactic ranking. It allows the user to provide an arbitrary ranking for the proof goals, specified in a language native to Tamarin. Each tactic needs to be given a name. For the tactic named default, the call would be {default}. The syntax of the tactics will be detailed below in the part Using a tactic. However, for a quick overview, a tactic is composed of several fields. The first one, tactic, specifies the name of the tactic and is mandatory. Then presort (optional) allows the user to choose the based ranking of the input. The keywords prio and deprio defines the ranks of the goals. They gather functions that will recognize the goals. The higher the prio that recognize a goal, the sooner it will be treated and the lower the deprio, the later. The user can choose to write as much of prio or deprio as needed. A tactic can also be composed of only prio or deprio. The functions are preimplemented and allow to reach information unavailable from oracle (the state of the system or the proof context).

o:

is the oracle ranking. It allows the user to provide an arbitrary program that runs independently of Tamarin and ranks the proof goals. The path of the program can be specified after the goal ranking, e.g., o "oracles/oracle-default" to use the program oracles/oracle-default as the oracle. If no path is specified, the default is oracle. The path of the program is relative to the directory of the protocol file containing the goal ranking. If the heuristic is specified using the --heuristic option, the path can be given using the --oraclename command line option. In this case, the path is relative to the current working directory. The oracle’s input is a numbered list of proof goals, given in the ‘Consecutive’ ranking (as generated by the heuristic C). Every line of the input is a new goal and starts with “%i:”, where %i is the index of the goal. The oracle’s output is expected to be a line-separated list of indices, prioritizing the given proof goals. Note that it suffices to output the index of a single proof goal, as the first ranked goal will always be selected. Moreover, the oracle is also allowed to terminate without printing a valid index. In this case, the first goal of the ‘Consecutive’ ranking will be selected.

O:

is the oracle ranking based on the ‘smart’ heuristic s. It works the same as o but uses ‘smart’ instead of ‘Consecutive’ ranking to start with.

p:

is the SAPIC-specific ranking. It is a modified version of the smart s heuristic, but resolves SAPIC’s state-facts right away, as well as Unlock goals, and some helper facts introduced in SAPICs translation (MID_Receiver, MID_Sender). Progress_To goals (which are generated when using the optional local progress) are also prioritised. Similar to fact annotations below, this ranking also introduces a prioritisation for Insert-actions When the first element of the key is prefixed F_, the key is prioritized, e.g., lookup <F_key,p> as v in .... Using L_ instead of F_ achieves deprioritsation. Likewise, names and be (de)prioritized by prefixes them in the same manner. See (Kremer and Künnemann 2016) for the reasoning behind this ranking.

P:

is like p but without delaying loop breakers.

If several rankings are given for the heuristic flag, then they are employed in a round-robin fashion depending on the proof-depth. For example, a flag --heuristic=ssC always uses two times the smart ranking and then once the ‘Consecutive’ goal ranking. The idea is that you can mix goal rankings easily in this way.

Fact annotations

Facts can be annotated with + or - to influence their priority in heuristics. Annotating a fact with + causes the tool to solve instances of that fact earlier than normal, while annotating a fact with - will delay solving those instances. A fact can be annotated by suffixing it with the annotation in square brackets. For example, a fact F(x)[+] will be prioritized, while a fact G(x)[-] will be delayed.

Fact annotations apply only to the instances that are annotated, and are not considered during unification. For example, a rule premise containing A(x)[+] can unify with a rule conclusion containing A(x). This allows multiple instances of the same fact to be solved with different priorities by annotating them differently.

When an In() premise is annotated, the annotations are propagated up to the corresponding !KU() goals. For example, the premise In(f(x))[+] will generate a !KU(f(x))[+] goal that will be solved with high priority, while the premise In(<y,g(y,z)>)[-] will generate !KU(y)[-] and !KU(g(y,z))[-] goals to be solved with low priority.

The + and - annotations can also be used to prioritize actions. For example, A reusable lemma of the form

    "All x #i #j. A(x) @ i ==> B(x)[+] @ j"

will cause the B(x)[+] actions created when applying this lemma to be solved with higher priority.

Heuristic priority can also be influenced by starting a fact name with F_ (for first) or L_ (for last) corresponding to the + and - annotations respectively. Note however that these prefixes must apply to every instance of the fact, as a fact F_A(x) cannot unify with a fact A(x).

Facts in rule premises can also be annotated with no_precomp to prevent the tool from precomputing their sources, and to prevent them from being considered during the computation of loop-breakers. Use of the no_precomp annotation allows the modeller to manually control how loops are broken, or can be used to reduce the precomputation time required to load large models. Note, however that preventing the precomputation of sources for a premise that is solved frequently will typically slow down the tool, as there will be no precomputed sources to apply. Using this annotation may also cause partial deconstructions if the source of a premise was necessary to compute a full deconstruction.

The no_precomp annotation can be used in combination with heuristic annotations by including both separated by commas—e.g., a premise A(x)[-,no_precomp] will be delayed and also will not have its sources precomputed.

Using a Tactic {subsec: tactic}

The tactics are a language native to Tamarin designed to allow user to write custom rankings of proof goals.

Writing a tactic

In order to explain the way a tactic should be written, we will use the simple example (theory SourceOfUniqueness). The first step is to identify the tactic by giving it a name (here uniqueness). Then you can choose a presort. It has the same role as the c or C option but with more options. Depending on whether you are using the diff mode are not, you will respectively be able to choose among ‘s’, ‘S’, ‘c’ and ‘C’ and ‘C’, ‘I’, ‘P’, ‘S’, ‘c’, ‘i’, ‘p’, ‘s’. Note that this field is optional and will by default be set at s.

tactic: uniqueness
presort: C

Then we will start to write the priorities following which we want to order the goals. Every priority, announced by the prio keywords, is composed of functions that will try to recognize characteristics in the goals given by the Tamarin proofs. If a goal is recognized by a function in a priority, it will be be ranked as such, i.e., the higher the priority in the tactic, the higher the goals it recognizes will be ranked. The particularity recognized by every function will be detailed in a paragraph below. The tactic language authorizes to combine functions using |, & and not. Even if the option is not necessary for the proof of the lemma uniqueness, let’s now explore the deprio keyword. It works as the prio one but with the opposite goal since it allows the user to put the recognized goals at the bottom of the ranking. In case several deprio are written, the first one will be ranked higher than the last ones. If a goal is recognized by two or more ‘priorities’ or ‘depriorities’, only the first one (i.e., the higher rank possible) will be taken into account for the final ranking. The order of the goals recognized by the same priority is usually predetermined by the presort. However, if this order is not appropriate for one priority, the user can call a ‘postranking function’. This function will reorder the goals inside the priority given a criteria. If no postranking function is determined, Tamarin will use the identity. For now, the only other option is smallest, a function that will order the goals by increasing size of their pretty-printed strings.

prio:
    isFactName "ReceiverKeySimple"
prio:
    regex "senc\(xsimple" | regex "senc\(~xsimple"
prio: {smallest}
    regex "KU\( ~key"
}

Calling a tactic

Like the other heuristics, tactics can be called two ways. The first one is using the command line. In the case study above, it would be: tamarin-prover --prove --heuristic={prove=uniqueness} SourceOfUniqueness.spthy. The other way is directly integrated in the file by adding [heuristic={uniqueness}] next to the name of the lemma that is supposed to use it. The option does not need to be called again from the command line. The second option is helpful when working with a file containing several tactics used by different lemmas.

Ranking functions

The functions used in the tactic language are implemented in Tamarin. Below you can find a list of the currently available functions. At the end at this section, you will find an explanation on how to write your own functions if the one described here do not suffice for your usage.

Pre-implemented functions * regex: as explain above, this function takes in parameter a string and will use it as a pattern to match against the goals. (Since it is based on the Text.Regex.PCRE module of Haskell, some characters, as the parenthesis, will need to be escaped to achieve the desired behavior). * isFactName: as is given by its name, this function will go look in the Tamarin object ‘goal’ and check if the field FactName matches its parameter. To give an example of its usage, isFactName could be used instead of regex for the first prio of the above example with same results. * isInFactTerms: the function will look in the list contained in the field FactTest whether an element corresponding the parameter can be found. The following functions are also implemented but specifically designed to translate the oracles of the Vacarme tool into tactics: * dhreNoise: recognize goals containing a Diffie-Hellman exponentiation. For example, the goal Recv( <'g'^~e.1,aead(kdf2(<ck, 'g'^(~e*~e.1)>), '0', h(<hash, 'g'^~e.1>), peer),aead(kdf2(<kdf1(<ck, 'g'^(~e*~e.1)>), z>), '0',h(<h(<hash, 'g'^~e.1>),aead(kdf2(<ck, 'g'^(~e*~e.1)>), '0', h(<hash, 'g'^~e.1>), peer)>), payload)>) ▶₁ #claim is recognized thanks to the presence of the following pattern 'g'^~e.1. The function does need one parameter from the user, the type of oracle it is used for. It can be def for the Vacarme default case, curve for Vacarme oracle_C25519_K1X1 case and diff if the tactic is used to prove an equivalence lemma. If the parameter specified is anything else, the default case will be used. It works as follows. First, it will retrieve from the system state the formulas that have the Reveal fact name and matches the regex exp\\('g'. For the retrieved formulas, it will then put in a list the content of the Free variables along the variable ~n. In the case of the example given above, the list would be [~n,~e,~e.1]. They are the variable that the function will try to match against. Once it is done, the tested goal will be recognized if it includes an exponentiation that uses the previously listed elements (just one as exponent or a multiplication).
* defaultNoise: this function takes two parameter: the oracle type (as explained for dhreNoise) and a regex pattern. The regex pattern should allow the program to extract the nonces targeted by the user from the goal. For example, in the default case of Vacarme, the regex is (?<!'g'\^)\~[a-zA-Z.0-9]* and aims at recovering the nonces used in exponentiation. The goal of the function is to verify that all the recovered nonces can be found in the list extracted from the system state as explained for dhreNoise. The goal will only be recognized if all his nonces are in the list. * reasonableNoncesNoise: takes one parameter (same as dhreNoise). It works as defaultNoise but works with all the nonces of the goal and therefore does not need a regex pattern to retrieve them. * nonAbsurdGoal: this function retrieve the functions names present in the goal and verifies if they are “Ku” or “inv” (this means the key words coming before parenthesis). It also retrieves the list of nonces form the system state as explained for dhreNoise and checks if they do not appear in the goal. If both the conditions are verified, the goal is recognized. It only takes one argument (the same as dhreNoise).

How to write your own function(s)

The functions need to be added to the lib/theory/src/Theory/Text/Parser/Tactics.hs file, in the function named tacticFunctions. The implementation has been designed to be modular. The first step is to record the function in the repertory, the name in quote will be the one used by the user in the tactic, the other, the one used for the implementation. They can be different if necessary. The “user function name” also need to be added to the nameToFunction list, along with a quick description for the error message. Regarding the implementation of the function, the first thing to know is that every function you write will take two parameters. The first one is the list of strings that the user may pass to the function (the pattern for regex for example). Nothing forbids the user to write as many parameters as he wants, we will however only use the first ones we need. The second parameter is a triplet composed of the goal being tested, the proof context and the system. The function then needs to return a boolean, True if the goal, proof context or system have been recognized, False if not. If needed, new postranking functions can be added by doing the following steps. First registering the name of the new function in the rankingFunctions function in lib/theory/src/Theory/Text/Parser/Tactics.hs. Then writing the function. It only needs to take in parameters the goals to sort and return them in the new order. To be considered, the code then needs to be recompiled, using make. The new function is then ready to be used.

Using an Oracle

Oracles allow to implement user-defined heuristics as custom rankings of proof goals. They are invoked as a process with the lemma under scrutiny as the first argument and all current proof goals seperated by EOL over stdin. Proof goals match the regex (\d+):(.+) where (\d+) is the goal’s index, and (.+) is the actual goal. A proof goal is formatted like one of the applicable proof methods shown in the interactive view, but without solve(…) surrounding it. One can also observe the input to the oracle in the stdout of tamarin itself. Oracle calls are logged between START INPUT, START OUTPUT, and END Oracle call.

The oracle can set the new order of proof goals by writing the proof indices to stdout, separated by EOL. The order of the indices determines the new order of proof goals. An oracle does not need to rank all goals. Unranked goals will be ranked with lower priority than ranked goals but kept in order. For example, if an oracle was given the goals 1-4, and would output:

4
2

the new ranking would be 4, 2, 1, 3. In particular, this implies that an oracle which does not output anything, behaves like the identity function on the ranking.

Next, we present a small example to demonstrate how an oracle can be used to generate efficient proofs.

Assume we want to prove the uniqueness of a pair <xcomplicated,xsimple>, where xcomplicated is a term that is derived via a complicated and long way (not guaranteed to be unique) and xsimple is a unique term generated via a very simple way. The built-in heuristics cannot easily detect that the straightforward way to prove uniqueness is to solve for the term xsimple. By providing an oracle, we can generate a very short and efficient proof nevertheless.

Assume the following theory.

theory SourceOfUniqueness begin

heuristic: o "myoracle"

builtins: symmetric-encryption

rule generatecomplicated:
 [ In(x), Fr(~key)  ]
 --[ Complicated(x) ]->
 [ Out(senc(x,~key)), ReceiverKeyComplicated(~key) ]

rule generatesimple:
 [ Fr(~xsimple), Fr(~key)  ]
 --[ Simpleunique(~xsimple) ]->
 [ Out(senc(~xsimple,~key)), ReceiverKeySimple(~key) ]

rule receive:
 [ ReceiverKeyComplicated(keycomplicated), In(senc(xcomplicated,keycomplicated))
 , ReceiverKeySimple(keysimple), In(senc(xsimple,keysimple))
 ]
 --[ Unique(<xcomplicated,xsimple>) ]->
 [  ]

//this restriction artificially complicates an occurrence of an event Complicated(x)
restriction complicate:
 "All x #i. Complicated(x)@i
   ==> (Ex y #j. Complicated(y)@j & #j < #i) | (Ex y #j. Simpleunique(y)@j & #j < #i)"

lemma uniqueness:
 "All #i #j x. Unique(x)@i & Unique(x)@j ==> #i=#j"

end

We use the following oracle to generate an efficient proof.

#!/usr/bin/env python

from __future__ import print_function
import sys

lines = sys.stdin.readlines()

l1 = []
l2 = []
l3 = []
l4 = []
lemma = sys.argv[1]

for line in lines:
  num = line.split(':')[0]

  if lemma == "uniqueness":
      if ": ReceiverKeySimple" in line:
        l1.append(num)
      elif "senc(xsimple" in line or "senc(~xsimple" in line:
        l2.append(num)
      elif "KU( ~key" in line:
        l3.append(num)
      else:
        l4.append(num)

  else:
    exit(0)

ranked = l1 + l2 + l3 + l4

for i in ranked:
  print(i)

Having saved the Tamarin theory in the file SourceOfUniqueness.spthy and the oracle in the file myoracle, we can prove the lemma uniqueness, using the following command.

tamarin-prover --prove=uniqueness SourceOfUniqueness.spthy

The generated proof consists of only 10 steps. (162 steps with ‘consecutive’ ranking, non-termination with ‘smart’ ranking).

Manual Exploration using GUI

See Section Example for a short demonstration of the main features of the GUI.

Different Channel Models

Tamarin’s built-in adversary model is often referred to as the Dolev-Yao adversary. This models an active adversary that has complete control of the communication network. Hence this adversary can eavesdrop on, block, and modify messages sent over the network and can actively inject messages into the network. The injected messages though must be those that the adversary can construct from his knowledge, i.e., the messages he initially knew, the messages he has learned from observing network traffic, and the messages that he can construct from messages he knows.

The adversary’s control over the communication network is modeled with the following two built-in rules:

rule irecv:
   [ Out( x ) ] --> [ !KD( x ) ]

rule isend:
   [ !KU( x ) ] --[ K( x ) ]-> [ In( x ) ]

The irecv rule states that any message sent by an agent using the Out fact is learned by the adversary. Such messages are then analyzed with the adversary’s message deduction rules, which depend on the specified equational theory.

The isend rule states that any message received by an agent by means of the In fact has been constructed by the adversary.

We can limit the adversary’s control over the protocol agents’ communication channels by specifying channel rules, which model channels with intrinsic security properties. In the following, we illustrate the modelling of confidential, authentic, and secure channels. Consider for this purpose the following protocol, where an initiator generates a fresh nonce and sends it to a receiver.

    I:  fresh(n)
    I -> R: n 

We can model this protocol as follows.

/* Protocol */

rule I_1: 
    [ Fr(~n) ]
    --[ Send($I,~n), Secret_I(~n) ]-> 
    [ Out(<$I,$R,~n>) ]
        
rule R_1:
    [ In(<$I,$R,~n>)  ]
    --[ Secret_R(~n), Authentic($I,~n) ]->
    [ ]

/* Security Properties */

lemma nonce_secret_initiator: 
    "All n #i #j. Secret_I(n) @i & K(n) @j ==> F"

lemma nonce_secret_receiver: 
    "All n #i #j. Secret_R(n) @i & K(n) @j ==> F"

lemma message_authentication: 
    "All I n #j. Authentic(I,n) @j ==> Ex #i. Send(I,n) @i &i<j"

We state the nonce secrecy property for the initiator and responder with the nonce_secret_initiator and the nonce_secret_receiver lemma, respectively. The lemma message_authentication specifies a message authentication property for the responder role.

If we analyze the protocol with insecure channels, none of the properties hold because the adversary can learn the nonce sent by the initiator and send his own one to the receiver.

Confidential Channel Rules

Let us now modify the protocol such that the same message is sent over a confidential channel. By confidential we mean that only the intended receiver can read the message but everyone, including the adversary, can send a message on this channel.

/* Channel rules */

rule ChanOut_C:
        [ Out_C($A,$B,x) ]
      --[ ChanOut_C($A,$B,x) ]->
        [ !Conf($B,x) ]

rule ChanIn_C:
        [ !Conf($B,x), In($A) ]
      --[ ChanIn_C($A,$B,x) ]->
        [ In_C($A,$B,x) ]

rule ChanIn_CAdv:
    [ In(<$A,$B,x>) ]
        -->
        [ In_C($A,$B,x) ]

/* Protocol */

rule I_1: 
    [ Fr(~n) ]
      --[ Send($I,~n), Secret_I(~n) ]-> 
    [ Out_C($I,$R,~n) ]
        
rule R_1:
    [ In_C($I,$R,~n)  ]
      --[ Secret_R(~n), Authentic($I,~n) ]->
    [ ]

The first three rules denote the channel rules for a confidential channel. They specify that whenever a message x is sent on a confidential channel from $A to $B, a fact !Conf($B,x) can be derived. This fact binds the receiver $B to the message x, because only he will be able to read the message. The rule ChanIn_C models that at the incoming end of a confidential channel, there must be a !Conf($B,x) fact, but any apparent sender $A from the adversary knowledge can be added. This models that a confidential channel is not authentic, and anybody could have sent the message.

Note that !Conf($B,x) is a persistent fact. With this, we model that a message that was sent confidentially to $B can be replayed by the adversary at a later point in time. The last rule, ChanIn_CAdv, denotes that the adversary can also directly send a message from his knowledge on a confidential channel.

Finally, we need to give protocol rules specifying that the message ~n is sent and received on a confidential channel. We do this by changing the Out and In facts to the Out_C and In_C facts, respectively.

In this modified protocol, the lemma nonce_secret_initiator holds. As the initiator sends the nonce on a confidential channel, only the intended receiver can read the message, and the adversary cannot learn it.

Authentic Channel Rules

Unlike a confidential channel, an adversary can read messages sent on an authentic channel. However, on an authentic channel, the adversary cannot modify the messages or their sender. We modify the protocol again to use an authentic channel for sending the message.

/* Channel rules */

rule ChanOut_A:
    [ Out_A($A,$B,x) ]
    --[ ChanOut_A($A,$B,x) ]->
    [ !Auth($A,x), Out(<$A,$B,x>) ]

rule ChanIn_A:
    [ !Auth($A,x), In($B) ]
    --[ ChanIn_A($A,$B,x) ]->
    [ In_A($A,$B,x) ]

/* Protocol */

rule I_1: 
    [ Fr(~n) ]
    --[ Send($I,~n), Secret_I(~n) ]-> 
    [ Out_A($I,$R,~n) ]
        
rule R_1:
    [ In_A($I,$R,~n)  ]
    --[ Secret_R(~n), Authentic($I,~n) ]->
    [ ]

The first channel rule binds a sender $A to a message x by the fact !Auth($A,x). Additionally, the rule produces an Out fact that models that the adversary can learn everything sent on an authentic channel. The second rule says that whenever there is a fact !Auth($A,x), the message can be sent to any receiver $B. This fact is again persistent, which means that the adversary can replay it multiple times, possibly to different receivers.

Again, if we want the nonce in the protocol to be sent over the authentic channel, the corresponding Out and In facts in the protocol rules must be changed to Out_A and In_A, respectively. In the resulting protocol, the lemma message_authentication is proven by Tamarin. The adversary can neither change the sender of the message nor the message itself. For this reason, the receiver can be sure that the agent in the initiator role indeed sent it.

Secure Channel Rules

The final kind of channel that we consider in detail are secure channels. Secure channels have the property of being both confidential and authentic. Hence an adversary can neither modify nor learn messages that are sent over a secure channel. However, an adversary can store a message sent over a secure channel for replay at a later point in time.

The protocol to send the messages over a secure channel can be modeled as follows.

/* Channel rules */

rule ChanOut_S:
        [ Out_S($A,$B,x) ]
      --[ ChanOut_S($A,$B,x) ]->
        [ !Sec($A,$B,x) ]

rule ChanIn_S:
        [ !Sec($A,$B,x) ]
      --[ ChanIn_S($A,$B,x) ]->
        [ In_S($A,$B,x) ]

/* Protocol */

rule I_1: 
    [ Fr(~n) ]
    --[ Send($I,~n), Secret_I(~n) ]-> 
    [ Out_S($I,$R,~n) ]
        
rule R_1:
    [ In_S($I,$R,~n)  ]
    --[ Secret_R(~n), Authentic($I,~n) ]->
    [ ]

The channel rules bind both the sender $A and the receiver $B to the message x by the fact !Sec($A,$B,x), which cannot be modified by the adversary. As !Sec($A,$B,x) is a persistent fact, it can be reused several times as the premise of the rule ChanIn_S. This models that an adversary can replay such a message block arbitrary many times.

For the protocol sending the message over a secure channel, Tamarin proves all the considered lemmas. The nonce is secret from the perspective of both the initiator and the receiver because the adversary cannot read anything on a secure channel. Furthermore, as the adversary cannot send his own messages on the secure channel nor modify messages transmitted on the channel, the receiver can be sure that the nonce was sent by the agent who he believes to be in the initiator role.

Similarly, one can define other channels with other properties. For example, we can model a secure channel with the additional property that it does not allow for replay. This could be done by changing the secure channel rules above by chaining !Sec($A,$B,x) to be a linear fact Sec($A,$B,x). Consequently, this fact can only be consumed once and not be replayed by the adversary at a later point in time. In a similar manner, the other channel properties can be changed and additional properties can be imagined.

Induction

Tamarin’s constraint solving approach is similar to a backwards search, in the sense that it starts from later states and reasons backwards to derive information about possible earlier states. For some properties, it is more useful to reason forwards, by making assumptions about earlier states and deriving conclusions about later states. To support this, Tamarin offers a specialised inductive proof method.

We start by motivating the need for an inductive proof method on a simple example with two rules and one lemma:

rule start:
  [ Fr(x) ]
--[ Start(x) ]->
  [ A(x) ]

rule repeat:
  [ A(x) ]
--[ Loop(x) ]->
  [ A(x) ]

lemma AlwaysStarts [use_induction]:
  "All x #i. Loop(x) @i ==> Ex #j. Start(x) @j"

If we try to prove this with Tamarin without using induction (comment out the [use_induction] to try this) the tool will loop on the backwards search over the repeating A(x) fact. This fact can have two sources, either the start rule, which ends the search, or another instantiation of the loop rule, which continues.

The induction method works by distinguishing the last timepoint #i in the trace, as last(#i), from all other timepoints. It assumes the property holds for all other timepoints than this one. As these other time points must occur earlier, this can be understood as a form of wellfounded induction. The induction hypothesis then becomes an additional constraint during the constraint solving phase and thereby allows more properties to be proven.

This is particularly useful when reasoning about action facts that must always be preceded in traces by some other action facts. For example, induction can help to prove that some later protocol step is always preceded by the initialization step of the corresponding protocol role, with similar parameters.

Induction, however, does not work for all types of lemmas. Let us investigate the limitations of induction now as well. Consider another rule and lemma, added to the model from above.

rule finish:
  [ A(x) ]
--[ End(x) ]->
  []

lemma AlwaysStartsWhenEnds [use_induction]:
  "All x #i. End(x) @i ==> Ex #j. Start(x) @j"

Tamarin will fail to prove the AlwaysStartsWhenEnds lemma, although we apply induction. The induction hypothesis here is that AlwaysStartsWhenEnds holds but not at the last time-point; or more detailed: If there is an End(x) but not at the last time-point, then there is a Start(x) but not at the last time-point.

We cannot apply this induction hypothesis fruitfully, though, as there will be always only one instance of End(~x), which will be at the last time-point. Intuitively speaking, induction can only be applied fruitfully if the facts, on which the lemma “depends” (e.g., on the left-hand side of an implication), occur multiple times in the trace. Usually, this applies to facts that “loop”.

Often, one can engineer around this restriction by connecting non-looping facts to looping facts using auxiliary lemmas. In the above example, the AlwaysStarts lemma provides such a connection. If you mark it as a reuse lemma, you can easily prove AlwaysStartsWhenEnds without induction.

Integrated Preprocessor

Tamarin’s integrated preprocessor can be used to include or exclude parts of your file. You can use this, for example, to restrict your focus to just some subset of lemmas, or enable different behaviors in the modeling. This is done by putting the relevant part of your file within an #ifdef block with a keyword KEYWORD

#ifdef KEYWORD
...
#endif

and then running Tamarin with the option -DKEYWORD to have this part included. In addition, a keyword can also be set to true with

#define KEYWORD

Boolean formulas in the conditional are also allowed as well as else branches

#ifdef (KEYWORD1 & KEYWORD2) | KEYWORD3
...
#else
...
#endif

If you use this feature to exclude source lemmas, your case distinctions will change, and you may no longer be able to construct some proofs automatically. Similarly, if you have reuse marked lemmas that are removed, then other following lemmas may no longer be provable.

The following is an example of a lemma that will be included when timethis is given as parameter to -D:

#ifdef timethis
lemma tobemeasured:
  exists-trace
  "Ex r #i. Action1(r)@i"
#endif

At the same time this would be excluded:

#ifdef nottimed
lemma otherlemma2:
  exists-trace
  "Ex r #i. Action2(r)@i"
#endif

The preprocessor also allows to include another file inside your main file.

#include "path/to/myfile.spthy"

The path can be absolute or relative to the main file. Included files can themselves contain other preprocessing flags, and the include behavior is recursive.

How to Time Proofs in Tamarin

If you want to measure the time taken to verify a particular lemma you can use the previously described preprocessor to mark each lemma, and only include the one you wish to time. This can be done, for example, by wrapping the relevant lemma within #ifdef timethis. Also make sure to include reuse and sources lemmas in this. All other lemmas should be covered under a different keyword; in the example here we use nottimed.

By running

time tamarin-prover -Dtimethis TimingExample.spthy --prove

the timing are computed for just the lemmas of interest. Here is the complete input file, with an artificial protocol:

/*
This is an artificial protocol to show how to include/exclude parts of
the file based on the built-in preprocessor, particularly for timing
of lemmas.
*/

theory TimingExample
begin

rule artificial:
    [ Fr(~f) ]
  --[ Action1(~f) , Action2(~f) ]->
    [ Out(~f) ]

#ifdef nottimed
lemma otherlemma1:
  exists-trace
  "Ex r #i. Action1(r)@i & Action2(r)@i"
#endif

#ifdef timethis
lemma tobemeasured:
  exists-trace
  "Ex r #i. Action1(r)@i"
#endif

#ifdef nottimed
lemma otherlemma2:
  exists-trace
  "Ex r #i. Action2(r)@i"
#endif

end

Configure the Number of Threads Used by Tamarin

Tamarin uses multi-threading to speed up the proof search. By default, Haskell automatically counts the number of cores available on the machine and uses the same number of threads.

Using the options of Haskell’s run-time system this number can be manually configured. To use x threads, add the parameters

+RTS -Nx -RTS

to your Tamarin call, e.g.,

tamarin-prover Example.spthy --prove +RTS -N2 -RTS

to prove the lemmas in file Example.spthy using two cores.

Equation Store

Tamarin stores equations in a special form to allow delaying case splits on them. This allows us for example to determine the shape of a signed message without case splitting on its variants. In the GUI, you can see the equation store being pretty printed as follows.

  free-substitution

  1. fresh-substitution-group
  ...
  n. fresh substitution-group

The free-substitution represents the equalities that hold for the free variables in the constraint system in the usual normal form, i.e., a substitution. The variants of a protocol rule are represented as a group of substitutions mapping free variables of the constraint system to terms containing only fresh variables. The different fresh-substitutions in a group are interpreted as a disjunction.

Logically, the equation store represents expression of the form

      x_1 = t_free_1
    & ...
    & x_n = t_free_n
    & ( (Ex y_111 ... y_11k. x_111 = t_fresh_111 & ... & x_11m = t_fresh_11m)
      | ...
      | (Ex y_1l1 ... y_1lk. x_1l1 = t_fresh_1l1 & ... & x_1lm = t_fresh_1lm)
      )
    & ..
    & ( (Ex y_o11 ... y_o1k. x_o11 = t_fresh_o11 & ... & x_o1m = t_fresh_o1m)
      | ...
      | (Ex y_ol1 ... y_olk. x_ol1 = t_fresh_ol1 & ... & x_1lm = t_fresh_1lm)
      )

Subterms

The subterm predicate (written << or ⊏) captures a dependency relation on terms. It can be used just as = in lemmas and restrictions. Intuitively, if x is a subterm of t, then x is needed to compute t. This relation is a strict partial order, satisfies transitivity, and, most importantly, is consistent with the equational theory. For example, x⊏h(x) and also c ++ a ⊏ a ++ b ++ c hold.

It gets more complicated when working with operators that are on top of a rewriting rule’s left side (excluding AC rules), e.g., fst/snd for pairs: fst(<a,b>) ↦ a, ⊕ for xor and adec/sdec for decryption. We call these operators reducible. These cases do not happen in practice as, it is not even clear what the relation intuitively means, e.g., for x⊏x⊕y one could argue that x was needed to construct x⊕y but if y is instantiated with x, then x⊕y=x⊕x=0 which clearly does not contain x.

Non-Provable Lemmas

Tamarins reasoning for subterms works well for irreducible operators. For reducible operators, however, the following situation can appear: No more goals are left but there are reducible operators in subterms. Usually, we have found a trace if no goals are left. However, if we have, e.g., x⊏x⊕y as a constraint left, then our constraint solving algorithm cannot solve this constraint, i.e., it is not clear whether we found a trace. In such a situation, Tamarin indicates with a yellow color in the proof tree that this part of the proof cannot be completed, i.e., there could be a trace, but we’re not sure. Even with such a yellow part, it can be that we find a trace in another part of the proof tree and prove an exists-trace lemma.

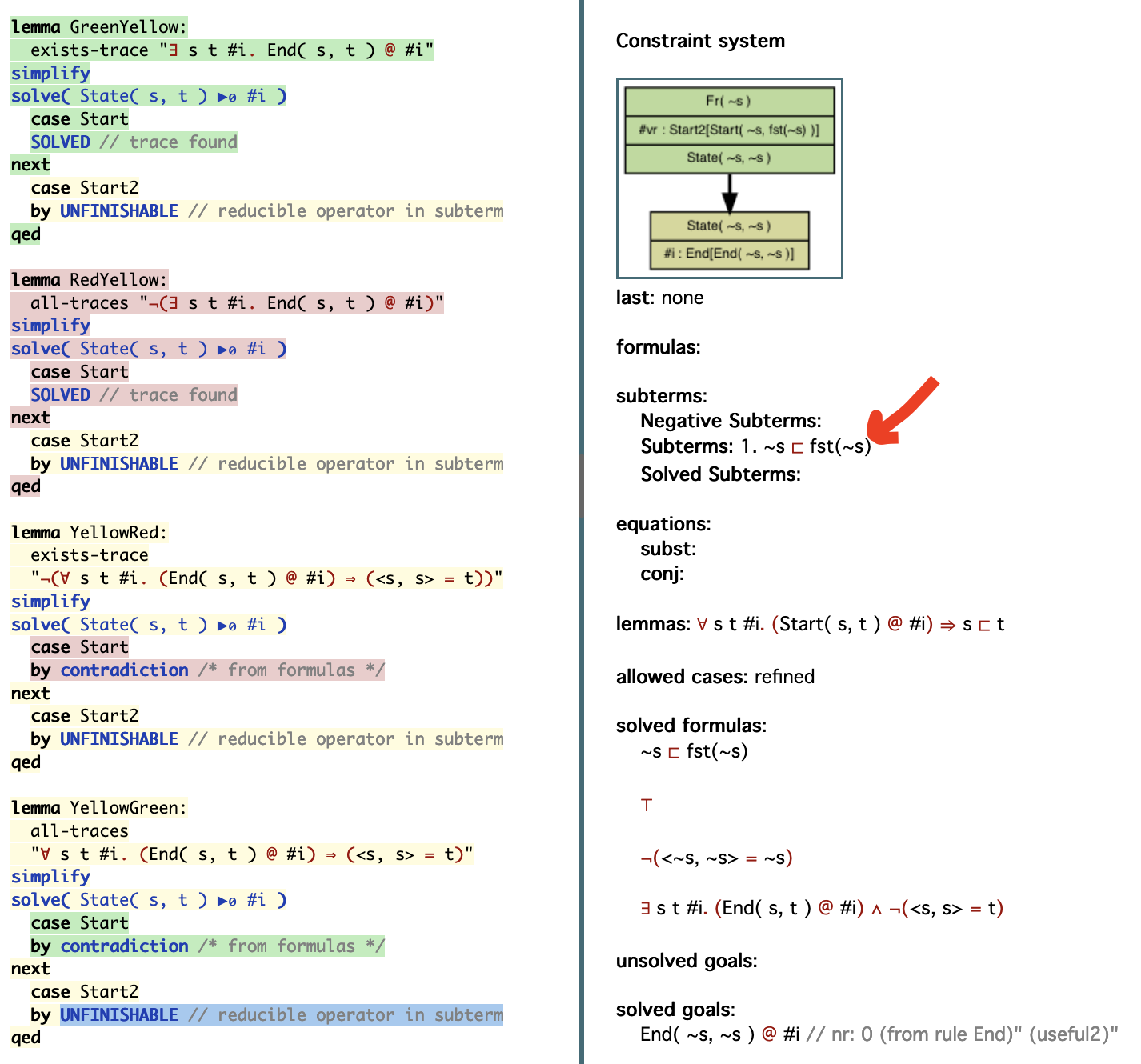
In the following picture one can see the subterm with the reducible operator fst on the right side. Therefore, on the left side, the proof is marked yellow (with the blue line marking the current position). Also, this example demonstrates in lemma GreenYellow, that in an exists-trace lemma, a trace can be still found and the lemma proven even if there is a part of the proof that cannot be finished. Analogously, lemma RedYellow demonstrates that a all-traces lemma can still be disproven if a violating trace was found. The last two lemmas are ones where no traces were found in the rest of the proof, thus the overall result of the computation is Tamarin cannot prove this property.

Subterm Store

Subterms are solved by recursively deconstructing the right side which basically boils down to replacing t ⊏ f(t1,...,tn) by the disjunction t=t1 ∨ t⊏t1 ∨ ··· ∨ t=tn ∨ t⊏tn. This disjunction can be quite large, so we want to delay it if not needed. The subterm store is the tool to do exactly this. It collects subterms, negative subterms (e.g., ¬ x ⊏ h(y) being split to x≠y ∧ ¬x⊏y) and solved subterms which were already split. With this collection, many simplifications can be applied without splitting, especially concerning transitivity.

Subterms are very well suited for nat terms as it reflects the smaller-than relation on natural numbers. Therefore, Tamarin provides special algorithms in deducing contradictions on natural numbers. Notably, if we are looking at natural numbers, we can deduce x⊏y from (¬y⊏x ∧ x≠y) which is not possible for normal subterms.

For more detailed explanations on subterms and numbers, look at the paper “Subterm-based proof techniques for improving the automation and scope of security protocol analysis” which introduced subterms and numbers to Tamarin.

Reasoning about Exclusivity: Facts Symbols with Injective Instances

We say that a fact symbol F has injective instances with respect to a multiset rewriting system R, if there is no reachable state of the multiset rewriting system R with more than one instance of an F-fact with the same term as a first argument. Injective facts typically arise from modeling databases using linear facts. An example of a fact with injective instances is the Store-fact in the following multiset rewriting system.

  rule CreateKey: [ Fr(handle), Fr(key) ] --> [ Store(handle, key) ]

  rule NextKey:   [ Store(handle, key) ] --> [ Store(handle, h(key)) ]

  rule DelKey:    [ Store(handle,key) ] --> []

When reasoning about the above multiset rewriting system, we exploit that Store has injective instances to prove that after the DelKey rule no other rule using the same handle can be applied. This proof uses trace induction and the following constraint-reduction rule that exploits facts with unique instances.

Let F be a fact symbol with injective instances. Let i, j, and k be temporal variables ordered according to

  i < j < k

and let there be an edge from (i,u) to (k,w) for some indices u and v, as well as an injective fact F(t,...) in the conclusion (i,u).

Then, we have a contradiction either if: 1) both the premises (k,w) and (j,v) are consuming and require a fact F(t,...). 2) both the conclusions (i,u) and (j,v) produce a fact F(t,..).

In the first case, (k,w) and (j,v) would have to be merged, and in the second case (i,u) and (j,v) would have to be merged. This is because the edge (i,u) >-> (k,w) crosses j and the state at j therefore contains F(t,...). The merging is not possible due to the ordering constraints i < j < k.

Detection of Injective Facts

Note that computing the set of fact symbols with injective instances is undecidable in general. We therefore compute an under-approximation to this set using the following simple heuristic:

We check for each occurrence of the fact-tag in a rule that there is no other occurrence with the same first term and 1. either there is a Fr-fact of the first term as a premise 2. or there is exactly one consume fact-tag with the same first term in a premise

We exclude facts that are not copied in a rule, as they are already handled properly by the naive backwards reasoning.

Additionally, we determine the monotonic term positions which are - Constant (=) - Increasing/Decreasing (</>) - Strictly Increasing/Decreasing (≤/≥) Positions can also be inside tuples if these tuples are always explicitly used in the rules.

In the example above, the key in Store is strictly increasing as key is a syntactic subterm of h(key) and h is not a reducible operator (not appearing on the top of a rewriting rules left side).

These detected injective facts can be viewed on the top of the right side when clicking on “Message Rewriting Rules”. The Store would look as follows: Store(id,<) indicating that the first term is for identification of the injective fact while the second term is strictly increasing. Possible symbols are ≤, ≥, <, > and =. A tuple position is marked with additional parantheses, e.g., Store(id,(<,≥),=).

Note that this support for reasoning about exclusivity was sufficient for our case studies, but it is likely that more complicated case studies require additional support. For example, that fact symbols with injective instances can be specified by the user and the soundness proof that these symbols have injective instances is constructed explicitly using the Tamarin prover. Please tell us, if you encounter limitations in your case studies: https://github.com/tamarin-prover/tamarin-prover/issues.

Monotonicity

With the monotonic term positions, we can additionally reason as follows: if there are two instances at positions i and j of an injective fact with the same first term, then - for each two terms s,t at a constant position - (1) s=t is deduced - for each two terms s,t at a strictly increasing position: - (2) if s=t, then i=j is deduced - (3) if s⊏t, then i<j is deduced - (4) if i<j or j<i, then s≠t is deduced - (5) if ¬s⊏t and ¬s=t, then j<i is deduced (as t⊏s must hold because of monotonicity) - for each two terms s,t at an increasing position: - (3) if s⊏t, then i<j is deduced - (5) if ¬s⊏t and ¬s=t, then j<i is deduced (as t⊏s must hold because of monotonicity) - for decreasing and strictly decreasing, the inverse of the increasing cases holds